Η "διακρίνουσα" είναι, ως γνωστόν, μετοχή ενεστώτα του ρήματος διακρίνω.
Διακρίνων-διακρίνουσα-διακρίνον! Και το ρήμα διακρίνω, που σημαίνει βλέπω, αντιλαμβάνομαι, ξεχωρίζω κλπ, είναι, ως γνωστόν, σύνθετο από την πρόθεση "δια" και το ρήμα "κρίνω", που σημαίνει νομίζω, αξιολογώ, εκτιμώ, ασκώ κριτική κλπ.
Επίσης, σχεδόν όλοι γνωρίζουν πως η Διακρίνουσα (Δ) στα Μαθηματικά είναι ένας πραγματικός αριθμός στενά συνυφασμένος με τη δευτεροβάθμια πολυωνυμική εξίσωση, καθώς το πρόσημό της μας βοηθά να διακρίνουμε, με όλες τις προαναφερθείσες σημασίες του ρήματος "διακρίνω", το πλήθος και το είδος των ριζών που έχει μια δευτεροβάθμια εξίσωση.
 Οι μαθητές διδάσκονται για πρώτη φορά τη δευτεροβάθμια εξίσωση, όταν φοιτούν στην τρίτη τάξη του Γυμνασίου και για δεύτερη φορά, όταν φοιτούν στην πρώτη τάξη του Λυκείου. Φτάνοντας μάλιστα στο Λύκειο πολλοί από αυτούς έχουν στο βαλιτσάκι της γνώσης που κουβαλούν μαζί τους το "βόδια στο τετράγωνο πλην τέσσερις αγελάδες", το οποίο μερικοί καθηγητές των Μαθηματικών συνηθίζουν να χρησιμοποιούν, για να βοηθήσουν τους μαθητές τους να απομνημονεύσουν τον τύπο που δίνει την αριθμητική τιμή της διακρίνουσας. Και φαίνεται πως η χρήση αυτού του εργαλείου επιφέρει καλό αποτέλεσμα, αλλά σε επίπεδο απομνημόνευσης και μόνο! Σχεδόν όλοι οι μαθητές θυμούνται τον τύπο της διακρίνουσας.
Οι μαθητές διδάσκονται για πρώτη φορά τη δευτεροβάθμια εξίσωση, όταν φοιτούν στην τρίτη τάξη του Γυμνασίου και για δεύτερη φορά, όταν φοιτούν στην πρώτη τάξη του Λυκείου. Φτάνοντας μάλιστα στο Λύκειο πολλοί από αυτούς έχουν στο βαλιτσάκι της γνώσης που κουβαλούν μαζί τους το "βόδια στο τετράγωνο πλην τέσσερις αγελάδες", το οποίο μερικοί καθηγητές των Μαθηματικών συνηθίζουν να χρησιμοποιούν, για να βοηθήσουν τους μαθητές τους να απομνημονεύσουν τον τύπο που δίνει την αριθμητική τιμή της διακρίνουσας. Και φαίνεται πως η χρήση αυτού του εργαλείου επιφέρει καλό αποτέλεσμα, αλλά σε επίπεδο απομνημόνευσης και μόνο! Σχεδόν όλοι οι μαθητές θυμούνται τον τύπο της διακρίνουσας.Αλλά αυτό είναι το ζητούμενο από τη διδασκαλία των Μαθηματικών; Η απομνημόνευση των τύπων;
Όχι πως προσωπικά είμαι κατά της απομνημόνευσης των μαθηματικών τύπων, ούτε των ρηματικών τύπων, ούτε ... των τύπων και των υπογραμμών, εν γένει, και δεν είμαι επειδή πιστεύω ότι όταν κάποιος αναγκάζεται από νεαρή ηλικία να ασκηθεί στην απομνημόνευση αναπτύσσει τις δικές του τεχνικές, που τον βοηθούν στην οργάνωση και διευθέτηση θεμάτων, στην κοινωνικοποίηση, στην πνευματική ανέλιξη κ.ά., ωστόσο στο θέμα των "βοδιών στο τετράγωνο ελαττωμένων κατά τέσσερις αγελάδες" έχω αναμφιβόλως τις αντιρρήσεις μου. Και ο λόγος που έχω τις αντιρρήσεις μου στη χρήση του συγκεκριμένου απομνημονευτικού κανόνα είναι ο τρόπος που αυτός εντυπώνεται στο κεφάλι των παιδιών! Μου φαίνεται πως το βάρος των βοδιών, και μάλιστα στο τετράγωνο(!), καίτοι ελαφρωμένο κατά το βάρος των τεσσάρων αγελάδων, δημιουργεί μια πολύ βαθιά χαρακιά στους ευαίσθητους εγκεφαλικούς νευρώνες των νεαρών μαθητών που δεν επουλώνεται ποτέ, με αποτέλεσμα όταν στη συνέχεια, καθώς το "τριώνυμο" και η δευτεροβάθμια εξίσωση δεν αποτελούν πλέον αυτοσκοπό, αλλά ένα χρήσιμο εργαλείο επίλυσης ποικίλων άλλων μαθηματικών προβλημάτων, να ξεπηδούν τα βόδια στο προσκήνιο και να ...οργώνουν εκεί που δεν τα σπέρνουν.:) Με αποτέλεσμα οι μαθητές να κάνουν χρήση του απομνηνονευτικού αυτού κανόνα και να υπολογίζουν αδιακρίτως μια Διακρίνουσα , όπου και όποτε συναντήσουν κάποια παράσταση που είτε είναι είτε θυμίζει τριώνυμο
δεύτερου βαθμού.
Σίγουρα δεν είμαι η μόνη που έχω προσέξει αυτό το φαινόμενο. Και δεν το πρόσεξα τώρα. Όμως με αφορμή μια συζήτηση που είχα με τον καλό μου συνάδελφο τον Φώτη, καθώς την Παρασκευή οδεύαμε από Θεσσαλονίκη προς Καρδίτσα για να πάρουμε μέρος στο 30ο Πανελλήνιο Συνέδριο της Ελληνικής Μαθηματικής Εταιρείας, αποφάσισα, επιστρέφοντας στο σχολείο, να καταγράψω μέσα από το μάθημα μερικά παραδείγματα "αντίδρασης" μαθητών στη θέα ενός τριωνύμου.
Σίγουρα δεν είμαι η μόνη που έχω προσέξει αυτό το φαινόμενο. Και δεν το πρόσεξα τώρα. Όμως με αφορμή μια συζήτηση που είχα με τον καλό μου συνάδελφο τον Φώτη, καθώς την Παρασκευή οδεύαμε από Θεσσαλονίκη προς Καρδίτσα για να πάρουμε μέρος στο 30ο Πανελλήνιο Συνέδριο της Ελληνικής Μαθηματικής Εταιρείας, αποφάσισα, επιστρέφοντας στο σχολείο, να καταγράψω μέσα από το μάθημα μερικά παραδείγματα "αντίδρασης" μαθητών στη θέα ενός τριωνύμου.
Σήμερα μου δόθηκε η ευκαιρία να το κάνω σε τρία διαφορετικά τμήματα και σε δυο διαφορετικές τάξεις. Στην Α' Λυκείου, στο μάθημα της Άλγεβρας και στη Β' Λυκείου, στα Μαθηματικά της Κατεύθυνσης.
Αντί για λόγια παραθέτω κάποιες από τις εικόνες που συνέλεξα.
Να σημειώσω πως δεν πρόκειται για τεστ, αλλά για φύλλο επανάληψης που το απάντησαν οι μαθητές συνεργαζόμενοι ανά δύο. Παρόμοια με την απάντηση της προηγούμενης εικόνας υπήρχε σε πολλά γραπτά. Για να συζητήσουμε το θέμα διεξοδικά, σήκωσα μια μαθήτρια στον πίνακα να γράψει τη δική της εκδοχή, η οποία φαίνεται στην επόμενη εικόνα:
(με πράσινο είναι οι υποδείξεις που έκανα εγώ, προσπαθώντας να βοηθήσω τη μαθήτρια)
Με αφορμή τη συζήτηση που ακολούθησε και τις διορθώσεις που έγιναν, κατασκεύασα επί τόπου μια πρόχειρη άσκηση, για να δω πώς θα αντιδράσουν οι μαθητές. Ζήτησα να προτείνουν λύσεις και κατέγραψα στον πίνακα τις τρεις προτάσεις (ή έστω τις δυο παρατηρήσεις και τη μια πρόταση) που ακούστηκαν:
Από τις δύο πρώτες (αυθόρμητες) παρατηρήσεις γίνεται προφανές πως το "τριώνυμο" είναι αυτό που "κλέβει την παράσταση" και αφήνει όλα τα υπόλοιπα στο παρασκήνιο.
Στην Α' Λυκείου δε το σημερινό μάθημα εξυπηρετούσε σε μεγάλο βαθμό τον πειραματισμό γύρω από το ερώτημα: "πώς αντιδρούν οι μαθητές στη θέα του τριωνύμου;".
Στην Α' Λυκείου δε το σημερινό μάθημα εξυπηρετούσε σε μεγάλο βαθμό τον πειραματισμό γύρω από το ερώτημα: "πώς αντιδρούν οι μαθητές στη θέα του τριωνύμου;".
Αφού έκανα μια σύντομη, πλην περιεκτική παράδοση, με αρκετές ερωταποκρίσεις και ο πίνακας μας είχε περίπου αυτήν τη μορφή:
ζήτησα από τους μαθητές να προσπαθήσουν να λύσουν την ακόλουθη άσκηση:

Περνώντας από τα θρανία, επιβεβαίωσα την πρόβλεψή μου! Η πλειοψηφία των μαθητών - και έχει πολύ καλούς, έξυπνους και μελετηρούς, μαθητές το συγκεκριμένο τμήμα της Α' - αντέδρασαν υπό την επήρεια του "βόδια στο τετράγωνο μείον τέσσερις αγελάδες"!
Με την άδειά τους φωτογράφησα μερικά τετράδια. Παραθέτω δυο χαρακτηριστικά ευρήματα:
Νομίζω πως τα ντοκουμέντα που παρέθεσα είναι αρκετά, για να επαληθεύσουν τον ισχυρισμό μου, ότι τελικά "τα βόδια στο τετράγωνο..." οργώνουν βαθιά τη σκέψη των μικρών μαθητών και τους καλλιεργούν μια αντανακλαστική αντίδραση όμοια με εκείνη του σκύλου στα πειράματα του Παυλόφ!
Και μπαίνει το ερώτημα: είναι τελικά σωστό χρησιμοποιώντας τόσο υπερμεγέθεις και ... υπέρβαρες εικόνες, όπως τα βόδια στο τετράγωνο και οι τέσσερις αγελάδες, να δημιουργούμε μια προκάτ αντίδραση στα παιδιά;
Μήπως αυτό περιορίζει την ικανότητά τους να "κρίνουν" και να διακρίνουν πού και πότε είναι χρήσιμο και απαραίτητο να υπολογίζουν τη Διακρίνουσα;
Θα με ενδιέφερε πολύ να έχω σχόλια, απόψεις, κρίσεις και απαντήσεις. :)
--------------------------------------------------------------------------------Θέλω να ευχαριστήσω όλους τους μαθητές μου, οι οποίοι έχοντας κατανοήσει την προσπάθεια που καταβάλω για να βρω τρόπους και πρακτικές που θα βελτιώσουν όσο το δυνατόν περισσότερο τη μαθηματική τους παιδεία, μου δείχνουν εμπιστοσύνη και μου επιτρέπουν να διαχειρίζομε ελεύθερα το υλικό που προκύπτει από τα μαθήματά μας στην τάξη του σχολείου.
Ελπίζω και εύχομαι με το τέλος της χρονιάς να έχουμε ξεκαθαρίσει το τοπίο και να έχουμε αποκτήσει επαρκή κρίση όλοι μας!



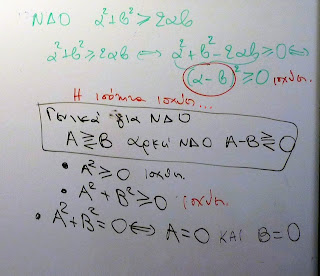



Και γιατί βρε Κατερίνα δεν προτιμάς να μιλήσουμε για τις έντονες παράλληλες πινελιές του μισότρελου Ligabue στο "όργωμα", ή για τα ανοιχτά στόματα των θηρίων που προτιμούσε να ζωγραφίζει, παρά μονάχα θέλεις να ανοίξουμε ολόκληρο θέμα με τη διακρίνουσα και τα συναφή;
ΑπάντησηΔιαγραφήΓιατί αν κάνουμε κάτι τέτοιο, τότε θα πρέπει να μιλήσουμε για την ελληνική μαθηματική ψευδο-εκπαίδευση: τη στείρα απομνημόνευση, τη μονότονη επανάληψη των θεμάτων απολυτήριων και προαγωγικών εξετάσεων, την απουσία πραγματικών προβλημάτων από την τάξη, τα βιβλία - αλμανάκ μαθηματικών θεσφάτων, τον εξοστρακισμό των νέων (και των παλαιών) τεχνολογιών, τα ιδιαίτερα μαθήματα (διορισμένων και μη), τα φροντιστήρια, τις πανελλαδικές, τα αποτελέσματα του διαγωνισμού PISA, την αγάπη για το αντικείμενο, την αγάπη για τους μαθητές, το ελληνικό σχολείο - τους πολίτες που αποζητά να παράξει, την ελληνική πολιτική σκηνή, τα μνημόνια, τα λαμόγια, το θολό αύριο, την ανασφάλεια, το μάταιο του πράγματος...
Αντ' αυτού προτείνω πέρα από όλα αυτά το "θερισμό" του Θεοφίλου Χατζημιχαήλ, σε αντίστοιχη ναΐφ τεχνοτροπία και θέμα.
Καλό βράδυ
Γεια σου Κώστα!
ΔιαγραφήΜου αρέσει ο σκωπτικός τρόπος που προσεγγίζεις το θέμα, στην αρχή τουλάχιστον.
Συμπτωματικά σήμερα σε ένα βιωματικό σεμινάριο που παρακολουθώ ένας εκ των συμμετεχόντων μας παρουσιάσει το βιβλίο του Μισεά, Η εκπαίδευση της αμάθειας. Το γνωρίζεις;
Όλα όσα αναφέρεις στη δεύτερη παράγραφο του σχολίου σου, κατά τον Μισεά είναι προδιαγεγραμμένα από το 1995 με συγκεκριμένο τρόπο, που αφορά την εκποίηση της παιδείας, και για συγκεκριμένο λόγο, που τον αντιλαμβάνεσαι.
Τώρα γιατί εγώ μιλάω για τη Διακρίνουσα; Απλούστατα, επειδή γι' αυτό είναι εύκολο να μιλήσω... :)
Καλό βράδυ.
Καλησπέρα.Δεν διαβάζω συχνά τις αναρτήσεις σου αλλά όταν τις διαβάζω αναπτερώνονται οι ελπίδες μου ότι δεν χάθηκαν όλα στη παιδεία.Είμαι μαθηματικός ,συνταξιούχος εδώ και λίγα χρόνια.Εφυγα με μειωμένη σύνταξη απογοητευμένη με όσα έβλεπα να συμβαίνουν στη παιδεία και ιδίως στ μαθηματικά.Οσα χρόνια δούλεψα πειραματίστηκα πολλές φορές στο να βρω ένα τρόπο να καταλάβουν και να αγαπήσουν τα μαθηματικά οσον το δυνατόν περισσότεροι μαθητές.Δούλεψα κυρίως σε γυμνάσιοκαι ειδικά στη Γ' γυμνασίου προσπαθούσα να τους προετοιμάσω για το λύκειο αλλά εις μάτην.Δεν μπόρεσα να καταλάβω τι εφταιγε.Τα παιδιά του γυμνασίου κάνουν ένα αγώνα δρόμου να πάρουν όσα πιο πολλά πτυχία ξένων γλωσσών για να μην τα έχουν στο λύκειο και χάνουν το γυμνάσιο .Θέλω να είμαι αισιόδοξη ότι θα φτιάξει η παιδεία μας γιατί μεγαλώνω εγγόνια κα θα ήθελα να έχουν μια σωστή παιδεία.
ΑπάντησηΔιαγραφήΚαλημέρα. Ευχαριστώ πολύ για τα ιδιαίτερα καλά σας λόγια.
ΔιαγραφήΝομίζω πως η κοινωνία γενικότερα τείνει να αλλάξει στάση απέναντι στο μαθηματικό αναλφαβητισμό, που μέχρι τώρα δεν τον θεωρούσε ιδιαίτερα αρνητικό ακόμη και για έναν καθόλα καλλιεργημένο άνθρωπο. Κι εγώ ελπίζω πως σταδιακά θα εδραιωθεί μια νέα αντίληψη σχετικά με τη μαθηματική παιδεία που οφείλει να έχει ο κάθε άνθρωπος που φοιτά στο σχολείο κι αυτό θα βοηθήσει στην αλλαγή στάσης των παιδιών και κυρίως των γονέων.
Να είσαστε καλά και να καμαρώνετε τα εγγόνια σας.
Ευχαριστώ και πάλι.
Πολυ καλα τα γραφεις Κατερινα!!! Και εγω κρινω οτι αδιακριτως και ακριτα χρησιμοποιουν την διακρινουσα οπουδηποτε μπορουν (ανεξαρτητα απο το εαν ειναι απαραιτητη ή οχι η χρηση της). Το θεμα ειναι οτι τα παιδια μαθαινουν να χρησιμοποιουν ο,τι μαθαινουν!!!
ΑπάντησηΔιαγραφήΗδη απο την προνηπιακη ηλικια οταν π.χ. ενα παιδακι μαθαινει να χρησιμοποιει το πιρουνι τοτε θα το χρησιμοποιησει καθε φορα που θα θελησει να φαει(ακομη και αν προκειται να φαει σουπα!!!) Το ιδιο αποδεικνυει περιτρανα και το κλασικο παραδειγμα γνωστο ως το προβλημα του καπετανιου που κοντολογις εχει ως εξης: "Δινεται οτι σε ενα καραβι πανω υπαρχουν 27 προβατα και 32 κατσικια. Ποια ειναι η ηλικια του καπετανιου;"
Αν θεσετε την ερωτηση αυτη σε παιδακια ηλικιας 9 χρονων τοτε τα 9 στα 10 θα απαντησουν οτι ο καπετανιος ειναι 59 ετων. Γιατι; Μα φυσικα επειδη γνωριζουν να κανουν προσθεση, επειδη "πιεζονται" να απαντησουν στο προβλημα και επειδη ο αριθμος 59 δεν ειναι εξωπραγματικος(ειναι μια λογικη ηλικια για εναν καπετανιο).
Το κακο συνεχιζεται και στο γυμνασιο οπως περιγραφεις με την διακρινουσα αλλα και στο λυκειο οπως παρατηρησα και στον φετινο μαθηματικο διαγωνισμο "Θαλη" στα θεματα της Γ λυκειου που ζητουσε καποιες ριζες μιγαδικης εξισωσης(δεν θυμαμαι ακριβως την εκφωνηση) και καποιοι μαθητες χρησιμοποιησαν το σχημα horner!!!
Το συμπερασμα ειναι οτι πραγματικα τα παιδια δεν μαθαινουν ποτε τους να σκεφτονται ορθα, λογικα και ορθολογικα! Προτιμαν να αντιμετωπιζουν τα προβληματα με μεθοδους "τυφλοσουρτη' χωρις να κατανοουν τι κανουν και γιατι.
Το που ακριβως οφειλεται αυτο ειναι αλλη μεγαλη ιστορια....
Με την ευκαιρια να σε ρωτησω και πως ηταν στο συνεδριο. Μπορουμε να βρουμε πουθενα την ομιλια σου για να την ακουσουμε;;;
Καλημέρα Δαμιανέ.
ΔιαγραφήΠράγματι είναι πολύ σύνθετο το αίτιο που προκαλεί αυτήν την αυτοματοποιημένη αντίδραση και υπάρχουν πολλές θεωρίες που προσπαθούν να την ερμηνεύσουν, αλλά ακόμη και σενάρια συνομωσίας περί συστηματικής καλλιέργειάς της. (Βλέπε για παράδειγμα το βιβλίο του Μισεά, "Η εκπαίδευση της αμάθειας" σε μετάφραση Άγγελου Ελεφάντη).
Στο Συνέδριο ήταν καλά. Την ομιλία μου δεν τη βιντεοσκόπησα εκεί, αλλά θα την επαναλάβω και θα τη βιντεοσκοπήσω τα Χριστούγεννα, για να την ανεβάσω στο διαδίκτυο. Νομίζω πως είναι μια καλή ιδέα η πρόταση που έκανα ειδικά για τους μαθηματικούς που διδάσκουν σε Γυμνάσιο. Αρκετοί από τους συναδέλφους που την άκουσαν στην Καρδίτσα μου είπαν πως θα το δοκιμάσουν στην πράξη. :)
(Αν στο μεταξύ θέλετε ίσως να την κάνω κάποια στιγμή άμεσα στο σχολείο, για όσους συναδέλφους ενδιαφέρονται. Σκέψου το και πες μου να το κανονίσουμε.)
Εξακολουθώ και υποστηρίζω την άποψη ότι πρέπει να μαθαίνουμε στα παιδιά περισσότερους από έναν-δύο-τρεις τρόπους να αντιμετωπίζουν τα προβλήματα. Και ταυτόχρονα να μην πιεζόμαστε -εμείς πρωτίστως- να "βγάλουμε την ύλη", ούτε να περνάμε αυτό το άγχος στα παιδιά. Η χρήση της διακρίνουσας έχει ξεφύγει εξαιρετικά - τη χρησιμοποιούν ακόμη και για την εξίσωση x^2 - 4 = 0 δηλαδή έλεος! Το ίδιο νοσηρό φαινόμενο είχα παρατηρήσει αρκετά χρόνια πριν, όταν είχα μια μαθήτρια από το Pinewood (με το αμερικάνικο σύστημα εκπαίδευσης) η οποία είχε τόσο υπερβολικά συνηθίσει (εθιστεί;) τη χρήση υπολογιστή τσέπης (κομπιουτεράκι το λεγόμενο) που έκανε πράξεις με αυτό ακόμη και όταν έλυνε την εξίσωση x - 2 = 5. Τραγικό; Για κείνη ήταν μονόδρομος - έλεγε: είμαι σίγουρη όταν το λύνω έτσι, ότι το κάνω σωστά. Το ίδιο μου απαντούν σήμερα μαθητές της Α΄ λυκείου και όχι μόνον (ειδικά όσοι είναι θεωρητική κατεύθυνση) - έχουν πειστεί ότι με αυτόν τον τρόπο (τη διακρίνουσα δλδ) το κάνουν πάντα σωστά. :( Κρίνω ότι δική μου δουλειά είναι να τους αποδείξω ότι η μέθοδος της διακρίνουσας και χρονοβόρα είναι και υπερβολική φήμη έχει και διευκολύνει εξαιρετικά τα λάθη. (σε παιδιά που βρίσκουν συνήθως το + και το - σχεδόν παρόμοια ή τα αγνοούν).
ΑπάντησηΔιαγραφήΚαι κάτι ακόμη: θα ήθελα οι συνάδελφοι που διδάσκουν στο γυμνάσιο και ειδικά στη Γ΄ να αφήσουν την "ευκολία" της διακρίνουσας και να μάθουν στα παιδιά παραγοντοποίηση. Στο δημοτικό βέβαια κάνουμε τη διαίρεση με διαδοχικές αφαιρέσεις - πόσο πιο κάτω;
ΔιαγραφήΣυμφωνώ Χριστίνα. Και επιπροσθέτως να πω ότι πιστεύω πως η γενικότερη ευκολία που έχει υιοθετεθεί τα τελευταία χρόνια σε όλες τις βαθμίδες της εκπαίδευσης έχει επιφέρει μεγάλη βλάβη στον τρόπο σκέψης και όχι μόνο στα Μαθηματικά. Η αδιάκριτη χρήση εννοιών, πράξεων-διαδικασιών, συμβόλων κλπ. είναι ένα φαινόμενο γενικευμένο και δεν αφορά μόνο το δικό μας μάθημα. Τα αίτιά του θα πρέπει να αναζητηθούν, υποθέτω, όχι αποκλειστικά και μόνο μέσα στο χώρο του σχολείου, αλλά παντού στην κοινωνία, με την ευρύτερη δυνατή σημασία της λέξης.
ΔιαγραφήΚαλημέρα!
Μια ενδιαφέρουσα απάντηση στο ερώτημά μου έδωσε ο συνάδελφος Γ. Καλαθάκης στο mathematica.gr, εδώ: http://www.mathematica.gr/forum/viewtopic.php?f=60&t=40967&p=190805#p190805
ΑπάντησηΔιαγραφήΜια μικρή παρατήρηση:
ΔιαγραφήΤο γ' πληθυντικό πρόσωπο είναι πολύ βολικό στη μετακύλιση των ευθυνών που βαραίνουν τους σχεδιαστές (αλλά και τους ίδιους τους εκπαιδευτικούς) ενός βάρβαρα αντιπαιδαγωγικού εκπαιδευτικού συστήματος, που έχει αποθεώσει την απομνημόνευση σε βάρος άλλων, ομολογουμένως σημαντικότερων, δεξιοτήτων.
Αν δεν ξεκινήσουμε να μιλούμε στο α' πληθυντικό πρόσωπο και δεν αναλογιστούμε τα σχεδιαστικά λάθη ενός συστήματος που δε δίνει τη δυνατότητα στους μαθητές να δομήσουν οι ίδιοι τις γνώσεις τους, στηριζόμενοι στα δικά τους λάθη και ανασκευές, τότε το μόνο που θα καταφέρνουμε είναι να κολλάμε τσιρότα σε αυτόν που έχει χάσει το πόδι του.
Εύστοχη η μικρή παρατήρηση.
ΔιαγραφήΆρα δεν μένει παρά να μας δώσεις και ένα, τουλάχιστον, παράδειγμα, για να κατανοήσουμε τι ακριβώς εννοείς στην πράξη.
Και η δική σου παρατήρηση επίσης εύστοχη. Ένα πρόχειρο πλάνο για μία εισαγωγή στη συνάρτηση y = α x^2 + β x + γ:
Διαγραφή1η φάση: Οι μαθητές συλλέγουν πληροφορίες για τον πληθυσμό ενός είδους υπό εξαφάνιση που τους ενδιαφέρει (κάτι που μπορεί να γίνει σε συνδυασμό με το μάθημα της Βιολογίας).
2η φάση: Τα δεδομένα εισάγονται σε λογιστικό φύλλο, γίνονται οι κατάλληλες γραφικές παραστάσεις. (Δουλεύονται οι διασυνδέσεις ανάμεσα στην εξαρτημένη και την ανεξάρτητη μεταβλητή)
3η φάση: Εισήγηση στη μοντελοποίηση δεδομένων με τη βοήθεια της β'θμιας πολυωνυμικής συνάρτησης.
4η φάση: Οι μαθητές κατασκευάζουν συναρτήσεις, βγάζουν συμπεράσματα για τον πληθυσμό που επέλεξαν να μελετήσουν. Κάνουν διασυνδέσεις ανάμεσα στις ιδιότητες της συνάρτησής τους (αύξουσα, φθίνουσα, κορυφή του γραφήματος, σημεία τομής του με τους άξονες, κλπ.) και το πραγματικό νόημά τους στο πρόβλημα που μελετούν. Οι ομάδες ετοιμάζουν τις παρουσιάσεις τους.
5η φάση: Η εργασία κάθε ομάδας παρουσιάζεται στην τάξη.
Παράλληλα οι ομάδες κρατούν ένα ημερολόγιο (ή ιστολόγιο) των εξερευνήσεών τους (νοητικών και μη), δίνοντας έμφαση στα μαθηματικά που τους δυσκολεύουν.
Αντιμετώπισα το πρόβλημα μάλλον πιο γενικά, αλλά πραγματικά πιστεύω πως η διδασκαλία της δευτεροβάθμιας απογυμνωμένη από πραγματικά προβλήματα (όπως το συγκεκριμένο, ή άλλα που μπορεί να βρει κανείς για παράδειγμα εδώ) στερείται νοήματος (συγνώμη, αλλά πραγματικά το πιστεύω).
O κ. Καλαθάκης έχει πραγματικά πολύ εύστοχα παραδείγματα! Ειδικά το πεδίο ορισμού της f με κλάσμα όπου ο αριθμητής θα... κάψει κόσμο! (;!)
ΔιαγραφήΚώστα κι εγώ πιστεύω ότι καμιά μαθηματική έννοια δεν πρέπει να πέφτει στο τραπέζι από το πουθενά.
ΑπάντησηΔιαγραφήΔυστυχώς όμως έτσι γίνεται.
Το σενάριό σου είναι πολύ καλό, και καθόλου εφαρμόσιμο στο Λύκειο.
Από καμιά άποψη όμως.
Απαιτεί τον επανασχεδιασμό όχι μόνο της δομής και της ύλης, αλλά και της ταξινόμησης.
Όμως τέτοιες ιδέες είναι εξαιρετικές για το μάθημα της Ερευνητικές Εργασίας ή για Καινοτόμες Δράσεις κλπ.
Ευχαριστώ και για τα σχόλια και για το υλικό. Όπως και να ΄χει είναι πολύ χρήσιμη η ανταλλαγή απόψεων και γνώσεων :)
υ.γ. Ειχα γράψει ένα εκτενές σχόλιο, με τις συμφωνίες μου και τις διαφωνίες μου, αλλά ο δαίμονας του υπολογιστή αποφάσισε να χαθεί...
Η Stella Baruk έχει ένα απολαυστικό (και ίσως αποκαρδιωτικό...) βιβλίο που λέγεται Si 7 = 0.
ΑπάντησηΔιαγραφήSi γαλλικά θα πει "αν", και ο τίτλος του βιβλίου προέρχεται ακριβώς από μία περίσταση όπου ζητήθηκε από παιδιά να λύσουν μια δευτεροβάθμια εξίσωση με αριθμητικούς συντελεστές· υπολόγισαν σωστά τη διακρίνουσα (που έβγαινε 7) και συνέχισαν ως εξής: "Αν 7>0, η εξίσωση έχει δύο ρίζες· αν 7=0, έχει μόνο μία· και αν 7<0, τότε δεν έχει."
Κάτι τέτοια η συγγραφέας τα ονομάζει προσφυέστατα automathismes. Δυστυχώς το λογοπαίγνιο δεν βγαίνει εξίσου ωραία στα ελληνικά.
Ευχαριστώ πολύ για την πληροφορία!
ΔιαγραφήΔεν το γνώριζα. Και είναι ιδιαίτερα παρήγορο,
επειδή οι δικοί μου οι μαθητές δεν φτάνουν σε αυτό το σημείο...
Αντιθέτως μερικοί, ευτυχώς ελάχιστοι, ανεξάρτητα από το πρόσημο του αριθμού με τον οποίο ισούται η διακρίνουσα, συνεχίζουν ακάθεκτοι για να υπολογίσουν ... τις πραγματικές ρίζες.
Ίσως αυτό αποτελεί ένα μικρό δείγμα για το ό,τι τον Έλληνα τίποτε δεν τον τρομάζει και τίποτε δεν το σταματά. :)
Να είσαστε καλά.