"Η ιδέα ενός τρυπανιού που ανοίγει σχεδόν τετράγωνες τρύπες εναντιώνεται στην κοινή λογική! Πώς είναι δυνατόν μια περιστρεφόμενη κεφαλή τρυπανιού να ανοίγει μη κυκλικές τρύπες;"
γράφει στη σελίδα 93 του βιβλίου "η λωρίδα του Μέμπιους", του Clifford Pickover, που κυκλοφορεί από τις εκδόσεις ΤΡΑΥΛΟΣ και που τυχαία άνοιξα στη σελίδα αυτή σήμερα το πρωί, περιμένοντας στο γραφείο του Διευθυντή. Προσπάθησα να φέρω στο μυαλό μου την κεφαλή του τρυπανιού και, καθώς διαθέτω δικό μου κρουστικό κι άρα έχω καλή σχέση με το εργαλείο, αναπαράστησα νοερά την κίνηση της κεφαλής και μια ολοστρόγγυλη τρύπα σχηματίστηκε στον ... αέρα, εκεί μπροστά στα μάτια μου! "Τελικά θα πρέπει να παραδεχτώ ότι η λογική μου δεν ξεφεύγει από την "κοινή" και γι' αυτό εναντιώνεται στις τετράγωνες τρύπες", σκέφτηκα και για να λύσω τον γρίφο της τετράγωνης οπής έπιασα να διαβάσω την παράγραφο από την αρχή:
"Τα μαθηματικά αξιοποιούνται και εφαρμόζονται στις ευρεσιτεχνίες με εντυπωσιακούς τρόπους: ένας από αυτούς είναι το τρίγωνο Ρελό - ένα τρίγωνο με καμπύλες πλευρές. Η συγκεκριμένη πατέντα με το τρίγωνο Ρελό αφορά κεφαλές τρυπανιών που μας βοηθούν να ανοίξουμε τετράγωνες τρύπες! [...] Η διατομή τους ορίζεται από το τρίγωνο Ρελό, το οποίο πήρε το όνομά του από τον διακεκριμένο μηχανολόγο μηχανικό Φραντς Ρελό (1829-1905)."
Στη συνέχεια μας παρέπεμπε σε εικόνα που παρίστανε το δίπλωμα
ευρεσιτεχνίας "Τρυπάνι για τετράγωνες τρύπες" (Δίπλ. Ευρ. ΗΠΑ 4.074.778) και συνέχιζε λέγοντας:
"Το ίδιο τρίγωνο εμφανίζεται και σε ευρεσιτεχνίες για άλλες κεφαλές τρυπανιών, καθώς και για καινοφανείς φιάλες, έλαστρα, κουτάκια αναψυκτικών, κεριά, ράφια που μπορούν να περιστραφούν, κιβώτια ταχυτήτων και ερμάρια. "
Μετά τον πρώτο ενθουσιασμό μου για το τρίγωνο Ρελό και καθώς το θέμα άρχισε να γίνεται εντελώς "μηχανικό" το ενδιαφέρον μου έτεινε να εξαντληθεί και προς στιγμή σκέφτηκα να κλείσω το βιβλίο και να περιμένω τον Διευθυντή άπραγη, αλλά τότε το μάτι μου πήρε τη λέξη "μαθηματικά" στην αμέσως επόμενη σειρά, οπότε, όπως ήταν φυσικό, κράτησα το βιβλίο ανοιχτό και συνέχισα να διαβάζω. Άλλωστε ο Διευθυντής είχε ακόμη πολλή δουλειά στο εργαστήριο της Φυσικής.
 "Για αναγνώστες που τους ενδιαφέρουν τα μαθηματικά, αναφέρουμε πως είναι εύκολο να κατασκευαστεί ένα τρίγωνο Ρελό. Αρχικά κατασκευάστε ένα ισόπλευρο τρίγωνο με πλευρά μήκους s. Στη συνέχεια με τη βοήθεια του διαβήτη, σχεδιάστε τρείς κύκλους με κέντρο καθεμία από τις κορυφές του τριγώνου και ακτίνα s. Τα τόξα που σχηματίζονται από τα σημεία τομής των τριών κύκλων και περνούν από τις κορυφές του αρχικού τριγώνου, αποτελούν τις πλευρές του τριγώνου Ρελό.
"Για αναγνώστες που τους ενδιαφέρουν τα μαθηματικά, αναφέρουμε πως είναι εύκολο να κατασκευαστεί ένα τρίγωνο Ρελό. Αρχικά κατασκευάστε ένα ισόπλευρο τρίγωνο με πλευρά μήκους s. Στη συνέχεια με τη βοήθεια του διαβήτη, σχεδιάστε τρείς κύκλους με κέντρο καθεμία από τις κορυφές του τριγώνου και ακτίνα s. Τα τόξα που σχηματίζονται από τα σημεία τομής των τριών κύκλων και περνούν από τις κορυφές του αρχικού τριγώνου, αποτελούν τις πλευρές του τριγώνου Ρελό.
Χάρη στις μελέτες πολλών μαθηματικών, γνωρίζουμε αρκετά για τις ιδιότητες του τριγώνου Ρελό. Το εμβαδόν του ισούται με:
και το εμβαδόν της περιοχής που διανοίγεται από ένα τέτοιο τρυπάνι καλύπτει το 0,9877003907...του εμβαδού ενός τετραγώνου. Η μικρή αυτή διαφορά οφείλεται στο ότι η κεφαλή του τρυπανιού Ρελό δημιουργεί τελικά ένα τετράγωνο με ελαφρώς στρογγυλεμένες κορυφές."
Η ενότητα για το τρίγωνο Ρελό τέλειωνε εδώ και η επόμενη ενότητα με τίτλο Η λωρίδα του Μέμπιους σε διάφορες ευρεσιτεχνίες ανέφερε διάφορα διπλώματα ευρεσιτεχνίας Μέμπιους, όπως για παράδειγμα του Όουεν Χάρις που του χορηγήθηκε ένα δίπλωμα ευρεσιτεχνίας το 1949, για έναν λειαντικό ιμάντα που αύξανε σημαντικά τη λειαντική ή στιλβωτική επιφάνεια..." κλπκλπ
Όσο προχωρούσα το διάβασμα άρχισα να σκέφτομαι πως το βιβλίο αυτό θα μπορούσε να χρησιμοποιηθεί ως βασικό εργαλείο στο μάθημα της ερευνητικής εργασίας! Ένα project που διασυνδέει τα Μαθηματικά και την Τεχνολογία, ιδανικός συνδυασμός με δυνατότητα ενεργοποίησης όλων των μαθητών ...Ενθουσιάστηκα δε ακόμη περισσότερο, όταν ανακάλυψα πως το 7ο κεφάλαιο έφερε τον πολλά υποσχόμενο τίτλο Παιχνίδια, λαβύρινθοι, τέχνη, μουσική και αρχιτεκτονική, ενώ το 8ο με τον τίτλο Λογοτεχνία και ταινίες ερχόταν για να υπερκαλύψει και όλα τα προσωπικά μου ενδιαφέροντα. Αυθόρμητα η σκέψη μου πλημμύρισε με εικόνες παιδιών που εργάζονταν σε τετραμελείς ομάδες, έχοντας κιόλας επιλέξει θέματα από τα πολλά που πρόσφερε το βιβλίο του Clifford Pickover, αλλά όταν τα βήματα του Διευθυντή αντήχησαν στο διάδρομο του άδειου από παιδιά σχολείου, επανήλθα με θλίψη στην ωμή πραγματικότητα...
Κάνω όνειρα για την επόμενη χρονιά, για το project και για τα μαθηματικά, ενώ δεν ξέρω πού θα βρίσκομαι την επόμενη σχολική χρονιά... Δεν μπορώ να προβλέψω πού θα με "ξεβράσει" η χαοτική κατάσταση που επικρατεί στον χώρο της παιδείας, και παντού, και γενικά...
Φοβάμαι μήπως οι γοητευτικές και πέρα από την κοινή λογική τετράγωνες τρύπες του Ρελό κι όλα τα σχέδια του project που έχω για του χρόνου στο μυαλό, αποδειχτούν στο τέλος μια ... τρύπα στο νερό.
---------------------------------------------------------------------------------------------------
Για περισσότερες πληροφορίες για το τρυπάνι Reuleaux δείτε εδώ "Est-il possible de forer des trous de forme carrée ?" και εδώ

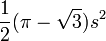

(Τ)ρελό)! Εξαιρετικό Κατερίνα! :-)
ΑπάντησηΔιαγραφήΈνα ωραίο στα τρίγωνα Ρελώ είναι πως σαν "καμπύλες σταθερού πλάτους" ενδείκνυνται για...καπάκια φρεατίων ,γιατί (όπως και οι κύκλοι) δεν πέφτουν μέσα στον ..εαυτό τους. :-)
ΑπάντησηΔιαγραφήΚαι για καπάκια από κατσαρόλες (αν και δεν έχω δει ακόμη (τ)ρελοκατσαρόλα, για νάμαι ειλικρινής..)
Παρεμπιπτόντως, νά μια ωραία ερώτηση για εξετάσεις Γεωμετρίας:
"Γιατί οι κατσαρόλες δεν είναι τετράγωνες;" Ποιος θα ξεχάσει το ρίζα2 μετά απ'αυτό; :-)
Ευχαριστώ Γιώργο! :)
ΑπάντησηΔιαγραφήΦέτος ρώτησα μια φορά σε τμήμα Γ' Λυκείου γιατί τα καπάκια των φρεατίων είναι στρογγυλά. Άκουσα απίστευτα αστείες και ασυνάρτητες απαντήσεις, ώσπου μια μαθήτρια θεωρητικής (με περίπου μηδενικό ενδιαφέρον για τα μαθηματικά) έδωσε τη σωστή απάντηση!
Ίσως πρέπει να βάζουμε και τέτοιες ερωτήσεις στις εξετάσεις, για να ενδιαφέρονται όλοι τελικά...
Και για να θυμούνται τη διαγώνιο του τετραγώνου, γιατί όχι και τον Ίππασο! :)
Καλό καλοκαίρι.
Το ιστολόγιο σας είναι πάρα πολύ ο΄μορφο, πλούσιο και ενδιαφέρον .Παρουσιάζει θέματα που μεέχουν ενθουσιάσει αφού έτσι βλέπω και μια άλλη ματιά τον μαθηματικών.Πήρα λοιπόν το θάρος και ανέβασα κάτι στο δικό μου ιστολόγιο προκειμένου να διαδώσω τις όμορφες ιδέες σας.
ΑπάντησηΔιαγραφήΚαραγιάννης Γιάννης
Σχολικός Σύμβουλος Μαθηματικών Ν. Δωδεκανήσου
Σας ευχαριστώ πολύ για τα καλά σας λόγια, κύριε Καραγιάννη. Και φυσικά ανταποδίδω τα συγχαρητήρια για το δικός σας πολύ πλούσιο και χρήσιμο ιστολόγιο.
ΔιαγραφήΜε τιμά ιδιαιτέρως που κάνατε ανάρτηση με παραπομπή στο blog μου.
Επίσης χαίρομαι πολύ όταν Σχολικοί Σύμβουλοι, όπως εσείς, βοηθούν στη διάδοση των Λεσχών Ανάγνωσης Μαθηματικής Λογοτεχνίας και γενικότερα στην καλλιέργεια της φιλαναγνωσίας.
Να είσαστε πάντα καλά.
Με εκτίμηση
ΚΚ
Τέτοιους συμβούλους θέλουμε!!
ΑπάντησηΔιαγραφήΓια πρισσότερες πληροφορίες:
ΑπάντησηΔιαγραφήReuleaux triangle
:)